石神井台・大泉南・上石神井・桃井・下井草・富士見ヶ丘・西荻窪・久米川の都立高校受験学習塾｜斗満学院TOMAN

中学1年生は現在『平面図形』を授業で扱っています。
その中でも「作図」はかなり重要です。
入試で必ず出題され、配点も高いですからね。

学校の授業に任せていると、結局何もわかっていない生徒さんが多いものです。
「作図は得意だ」と思っている生徒さんでも、
なんとなく適当に作図を組み合わせて偶然合っているだけ、なんてケースも結構あります。

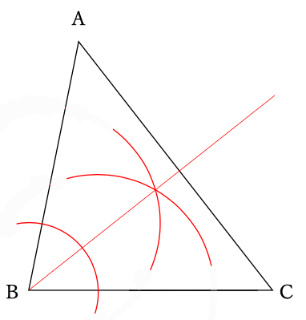
理解度を確かめる例題として、下図のような△ABCについて考えてみましょう。


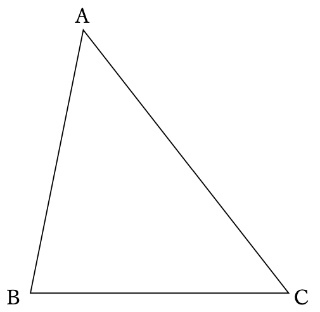
その上で、
(1)点Aと点Cが重なるように折った時の線を作図しなさい。
(2)辺ABと辺BCが重なるように折った時の線を作図しなさい。
(3)底辺をACとした時の三角形の高さを作図しなさい。

これらの問題の区別が全くできない生徒さんが多いんですよ。

作図で基本となるものは全部で３種類。
①垂直二等分線　
②角の二等分線　
③垂線です。

それぞれに表現としての意味があるにもかかわらず、とりあえず垂直なら①、みたいに皆さん描きがちです。
垂直だけを表現したいのであれば、正しくは③を使用しなければいけないんですけどね。
そもそも「線」とは「点」の集合体。
それぞれが位置関係を持っているものだという前提で理解しなければなりません。

(1)の答えは、「２つの点からの距離が等しい点の集合体」として下図の垂直二等分線が正答になります。
ポイントとしては、点Aと点Cとの位置関係なので、点Bは通らないことです。



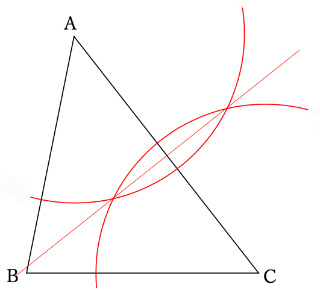
(2)の答えは、「２つの辺からの距離が等しい点の集合体」として下図の角の二等分線が正答になります。
ポイントとしては、ACの中点を通らず、ACと垂直関係にもないことです。


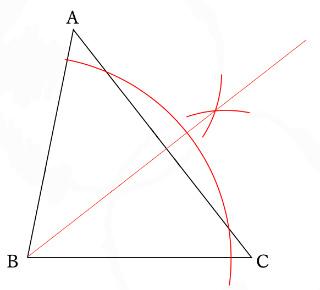
(3)の答えは、「点Bを通るACに垂直な線」を書く必要があるので、下図の垂線が正答になります。

作図はテキトー禁止。常に論理的に。僕の口癖です。

今回はかなり講義っぽいブログになりましたが、
TOMAN久米川教室では授業内でも上記のように説明をして、反復・確認テストをしています。

一応、現中学1年生は全員テストを合格していますので、次回の定期テストの作図には期待しています。
もちろん、冬休み中も確認しますね！