カテゴリ
月別 アーカイブ
- 2025年4月 (4)
- 2025年3月 (65)
- 2025年2月 (59)
- 2025年1月 (61)
- 2024年12月 (64)
- 2024年11月 (65)
- 2024年10月 (67)
- 2024年9月 (65)
- 2024年8月 (62)
- 2024年7月 (66)
- 2024年6月 (67)
- 2024年5月 (65)
- 2024年4月 (63)
- 2024年3月 (64)
- 2024年2月 (56)
- 2024年1月 (52)
- 2023年12月 (54)
- 2023年11月 (55)
- 2023年10月 (53)
- 2023年9月 (54)
- 2023年8月 (54)
- 2023年7月 (57)
- 2023年6月 (62)
- 2023年5月 (76)
- 2023年4月 (89)
- 2023年3月 (85)
- 2023年2月 (69)
- 2023年1月 (69)
- 2022年12月 (70)
- 2022年11月 (65)
- 2022年10月 (51)
- 2022年9月 (44)
- 2022年8月 (20)
- 2022年7月 (35)
- 2022年6月 (37)
- 2022年5月 (37)
- 2022年4月 (50)
- 2022年3月 (42)
- 2022年2月 (51)
- 2022年1月 (37)
- 2021年12月 (42)
- 2021年11月 (41)
- 2021年10月 (37)
- 2021年9月 (20)
- 2021年8月 (25)
- 2021年7月 (28)
- 2021年6月 (20)
- 2021年5月 (27)
- 2021年4月 (83)
- 2021年3月 (59)
- 2021年2月 (15)
- 2021年1月 (36)
- 2020年12月 (44)
- 2020年11月 (46)
- 2020年10月 (47)
- 2020年9月 (39)
- 2020年8月 (47)
- 2020年7月 (73)
- 2020年6月 (77)
- 2020年5月 (26)
- 2020年4月 (53)
- 2020年3月 (84)
- 2020年2月 (35)
- 2020年1月 (29)
- 2019年12月 (36)
- 2019年11月 (34)
- 2019年10月 (35)
- 2019年9月 (29)
- 2019年8月 (26)
- 2019年7月 (46)
- 2019年6月 (68)
- 2019年5月 (86)
- 2019年4月 (111)
- 2019年3月 (143)
- 2019年2月 (88)
- 2019年1月 (90)
- 2018年12月 (101)
- 2018年11月 (52)
- 2018年10月 (64)
- 2018年9月 (70)
- 2018年8月 (96)
- 2018年7月 (80)
- 2018年6月 (49)
- 2018年5月 (50)
- 2018年4月 (48)
- 2018年3月 (53)
- 2018年2月 (36)
- 2018年1月 (48)
- 2017年12月 (36)
- 2017年11月 (48)
- 2017年10月 (55)
- 2017年9月 (58)
- 2017年8月 (65)
- 2017年7月 (88)
- 2017年6月 (97)
- 2017年5月 (107)
- 2017年4月 (109)
- 2017年3月 (117)
- 2017年2月 (104)
- 2017年1月 (95)
- 2016年12月 (69)
- 2016年11月 (4)
- 2016年10月 (5)
最近のエントリー
HOME > 教室長ブログ > 久米川教室 > 3/3【久米川教室】展開を笑うものは展開に泣く
久米川教室
< 3/3【富士見ヶ丘教室】岡田より | 一覧へ戻る | 3/4【久米川教室】スタート >
3/3【久米川教室】展開を笑うものは展開に泣く
昨日は新中3クラスで最初の数学。
内容としては「展開」という中2でも扱った単項式・多項式の計算です。
新中3生は「証明」や「確率」などを扱う中2の冬に入塾した生徒さんが多いので、
各自の「文字式」を扱う基礎計算力を測る機会に恵まれませんでした。
昨日の授業でそのあたりを見させてもらったのですが、怪しい生徒さんがチラホラ。
計算力として求められるものは2つ。
「暗算の正確さ」と「途中式の正確さ」です。
人によって目指すべき配分が異なります。
大多数の子は暗算:途中式を3:7くらいの割合で錬成していくべきです。
TOMANは途中式にうるさい塾です。
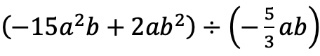
上記のような問題で、すぐに答えを書こうとする子は厳重注意です。
計算における複数の作業を一度に処理しようと試みているからです。
複数作業というのは、
①符号処理、②約分、③係数の乗除、④同類項まとめ、などを指します。
これらを一度にやろうとする子って、
よほど「頭が良い」か「面倒くさがり」で、9割は後者に該当します。
そしてその9割の子は高確率でミスをします。
同時に複数の作業をできる人間なんて、ごく一部に限られますからね。
「途中式は長ければ長いほどかっこいい」
授業中の合言葉です。
知っての通り、都立一般入試の数学では上記のような計算が出題されます。
しかも配点は共通校で5点。自校であれば6点だったりします。
「面倒くさい」という感情で、5点も6点も失点。
しかもそのせいで不合格なんてことがあったら悲惨ですよ。
これまでの怠惰な計算のやり方とは決別して、丁寧さを心がけてくださいね。
内容としては「展開」という中2でも扱った単項式・多項式の計算です。
新中3生は「証明」や「確率」などを扱う中2の冬に入塾した生徒さんが多いので、
各自の「文字式」を扱う基礎計算力を測る機会に恵まれませんでした。
昨日の授業でそのあたりを見させてもらったのですが、怪しい生徒さんがチラホラ。
計算力として求められるものは2つ。
「暗算の正確さ」と「途中式の正確さ」です。
人によって目指すべき配分が異なります。
大多数の子は暗算:途中式を3:7くらいの割合で錬成していくべきです。
TOMANは途中式にうるさい塾です。
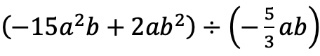
上記のような問題で、すぐに答えを書こうとする子は厳重注意です。
計算における複数の作業を一度に処理しようと試みているからです。
複数作業というのは、
①符号処理、②約分、③係数の乗除、④同類項まとめ、などを指します。
これらを一度にやろうとする子って、
よほど「頭が良い」か「面倒くさがり」で、9割は後者に該当します。
そしてその9割の子は高確率でミスをします。
同時に複数の作業をできる人間なんて、ごく一部に限られますからね。
「途中式は長ければ長いほどかっこいい」
授業中の合言葉です。
知っての通り、都立一般入試の数学では上記のような計算が出題されます。
しかも配点は共通校で5点。自校であれば6点だったりします。
「面倒くさい」という感情で、5点も6点も失点。
しかもそのせいで不合格なんてことがあったら悲惨ですよ。
これまでの怠惰な計算のやり方とは決別して、丁寧さを心がけてくださいね。
カテゴリ:
(TOMAN)
< 3/3【富士見ヶ丘教室】岡田より | 一覧へ戻る | 3/4【久米川教室】スタート >