教室長ブログ
11/30【久米川教室】証明って楽しい②
現在、中学2年生は数学の授業にて「証明」を扱っています。
以前もブログ(2020/12/27)に書いたことなのですが、
「証明って本当に楽しい」です。
例題:△ABCの辺BCの中点をMとする。
線分AMをMの方向に延ばした直線と頂点Bを通り辺ACに平行な直線との交点をDとすると,CA=BDであることを証明せよ。
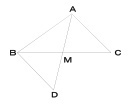
この問題、結論はCA=BDで、辺の長さが等しいことを証明するものです。
僕は毎回生徒さんたちに質問します。
答えは「その辺や角を含む合同と思われる三角形を探す」です。
この場合、△ABCと△BADで検討してそこで止まってしまう生徒さんは惜しいです。
正直こういう生徒さんは、いつも解答を写しているだけで何も考えられていない状態です。
そういう子に限って、途中対応順めちゃくちゃ、全然関係ない辺や角について論じ始める始末。
こういう子たちは日頃の言動においても根拠のないことを言いがちだったり、何も考えずに行動しがちだったりします。
周りの大人がいちいち行動を促すのではなく、自分で意図や目的を考えさせて色々取り組ませないとダメですね。
「証明」はそれを学ぶのにもってこいの単元であるといえます。
TOMANでは思考段階において未熟な生徒さんにとことん時間をかけます。
以前もブログ(2020/12/27)に書いたことなのですが、
「証明って本当に楽しい」です。
例題:△ABCの辺BCの中点をMとする。
線分AMをMの方向に延ばした直線と頂点Bを通り辺ACに平行な直線との交点をDとすると,CA=BDであることを証明せよ。

この問題、結論はCA=BDで、辺の長さが等しいことを証明するものです。
僕は毎回生徒さんたちに質問します。
「辺の長さや角の大きさが等しいことを証明したいとき、何から始めるか。」
答えは「その辺や角を含む合同と思われる三角形を探す」です。
この場合、△ABCと△BADで検討してそこで止まってしまう生徒さんは惜しいです。
根拠に基づいて合同かどうか検討して、ダメなら却下。
△ABCと△BADだと合同とは言い切れません。
他の三角形で検討するべきです。
△ABCと△BADだと合同とは言い切れません。
他の三角形で検討するべきです。
今回だと△ACMと△DBMを選べた生徒さんが正解。
その後もしっかり書けていました。
それなのに、わけもわからず「仮定より」から書き始める生徒さんもチラホラ。
その後もしっかり書けていました。
試行錯誤を経て方針が立った段階で、いよいよ証明を書き始めるのが王道なわけです。
正直こういう生徒さんは、いつも解答を写しているだけで何も考えられていない状態です。
そういう子に限って、途中対応順めちゃくちゃ、全然関係ない辺や角について論じ始める始末。
いちいち根拠がないことを平気で書いてしまうんですね。
さらに「結論」を「仮定」扱いして等式を書くいう証明する上での1番のタブーまで散見されました。
こういう子たちは日頃の言動においても根拠のないことを言いがちだったり、何も考えずに行動しがちだったりします。
周りの大人がいちいち行動を促すのではなく、自分で意図や目的を考えさせて色々取り組ませないとダメですね。
「証明」はそれを学ぶのにもってこいの単元であるといえます。
TOMANでは思考段階において未熟な生徒さんにとことん時間をかけます。
ここから2月の学年末までに冬期講習の時間も含めてじっくり「論理的思考力」みたいなものを叩き込んでいくつもりです。
